Fragen:

1. Wann haben zwei Mengen ein- und dieselbe Elementzahl ("Mächtigkeit")?
2. Wann ist eine Menge endlich / unendlich?
3. Gibt es verschiedene "Qualitäten" von unendlicher Mächtigkeit?

a  3
b  2
c  1

Es seien A, B Mengen. Dann heißt A gleichmächtig zu B ( Schreibweise: A  B bzw. # A = # B ) genau dann, wenn eine 1-1-Zuordnung von A auf B (sogenannte Bijektion von A auf B) existiert.

Definition 2: (Endlichkeitsdefinition nach R. Dedekind (1831 - 1916))

1. Eine Menge M heißt endlich genau dann, wenn  ( M'  M  M'  M )
2. Eine Menge M heißt unendlich, wenn sie nicht endlich ist.
3. Die Mächtigkeit der leeren Menge ist gleich Null ( # =0 ).

1. ,  sind unendlich.



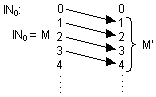
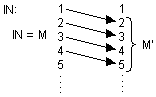
Folgerung: ;  G (gerade Zahlen);  U (ungerade Zahlen)
 

2.          0    1    2    3    4    5    .......

                  0    1   -1    2   -2    3    .......

n

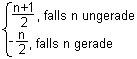
daraus folgt: die Mächtigkeit der Menge  ist eine typische Mächtigkeit für unendliche Mengen

Mit  (aleph-null) bezeichnen wir die Mächtigkeit der Menge . Ist eine Menge M gleichmächtig zu , so nennen wir M abzählbar unendlich und schreiben # M = .

Folgerung:  #  = # U = # G = # P = #  =    (P - Menge aller Primzahlen)

Satz 1: Die Menge aller Paare natürlicher Zahlen ist abzählbar unendlich ( # (  ) = # ² = #  =  ).

Beweis: Wir geben eine Bijektion von  auf  an:

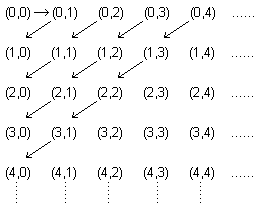
Bijektion C:
 

C:	(0,0)	(0,1)	(1,0)	(0,2)	(1,1)	(2,0)	(0,3)	(1,2)	(2,1)	(3,0)	(0,4)	......
	0	1	2	3	4	5	6	7	8	9	10	......

 
Zuordnungsvorschrift:

C heißt "Cantornummerierung"
Umkehrfunktionen l und r zu dieser Cantornummerierung:   (....noch zu ergänzen)

Folgerung 1:

Auch die Menge aller geordneten Tripel natürlicher Zahlen und allgemein die Menge aller geordneten s-Tupel natürlicher Zahlen ist abzählbar unendlich. ( s > 2, s  ) ( # ³ = # ^S =  )

Beweisidee:

Die Cantornummerierung der Menge aller Tripel natürlicher Zahlen erhalten wir zum Beispiel durch den Ansatz:

C₃ (m,n,k) = C (m,C(n,k))

C₁³ (z) = l (z)
C₂³ (z) = l (r(z))
C₃³ (z) = r (r(z))

Folgerung 2:

Die Menge  aller rationalen Zahlen ist abzählbar unendlich, das heißt #  =  bzw. .

Beweis:Wir geben eine Bijektion von  auf  an:

• erster Wert = 0 wählen
• nachdem eine rationale Zahl aus dem Schema in der Nummerierung auftaucht, folgt unmittelbar ihr negativer Wert
• Zahlen, die vorangegangen gleich sind (ungekürzte Brüche), werden übergangen

Satz 2: (Cantor 1874)

Das reelle Intervall (0,1) = {x: x  0 < x < 1 } ist nicht abzählbar unendlich, das heißt # (0,1)  bzw. (0,1) .

Bemerkung:

Die Mächtigkeit von (0,1) ist "größer" als die der natürlichen Zahlen, sie wird die Mächtigkeit des Kontinuums genannt und mitbezeichnet.

Beweis:

Jede reelle Zahl aus (0,1) hat die Form 0,a₁a₂a₃... mit a_i.
Annahme: (0,1) , das heißt es gäbe eine Bijektion von  auf (0,1).
                Das heißt, es gibt eine Nummerierung all dieser reellen Zahlen:

0, a₁₁  a₁₂  a₁₃  a₁₄  a₁₅  ...
0, a₂₁  a₂₂  a₂₃  a₂₄  a₂₅  ...
0, a₃₁ a₃₂  a₃₃  a₃₄  a₃₅  ...

Nach Konstruktion gilt d  (0,1), aber d unterscheidet sich von jeder Zahl in der obigen Nummerierung (in mindestens der i-ten Stelle nach dem Komma). Dies steht jedoch im Widerspruch zur Annahme!

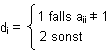
Folgerung:

Jedes reelle Intervall (a,b) ( a < b; a,b  ) sowie die gesamte Menge der reellen Zahlen ist zu (0,1) gleichmächtig.

Hierarchie der Zahlenklassen:

Gibt es weitere unendliche Mächtigkeiten außer  und ?

Satz 3: (Satz von Cantor)

Es existiert keine Menge A mit A  P(A). Das heißt, für alle Mengen A gilt A  P(A).

Folgerung:

Durch Potenzmengenbildung entstehen stets neue ("höhere") Mächtigkeiten.
zum Beispiel:  P() ;  P()  P(P())  P(P(P()))

indirekter Beweis des Satzes von Cantor:

Annahme: Es existiert eine Menge A derart, daß A  P(A).
                Das heißt, es existiert eine Bijektion f:A  P(A)
                Dann bilden wir die Menge X = { x: x  A x  f(x) }  A. Dann gilt X P(A).
                Dann existiert (genau) ein a₀ A mit f(a₀) = X.
                Dann gilt a₀ X a₀ A  a₀ f(a₀)  a₀ X
Dies ist ein Widerspruch, die Annahme ist also falsch und der Satz damit bewiesen.

Die Cantorsche Mengenlehre wird auch als "naive Mengenlehre" bezeichnet. Grund: Sie läßt logische Antinomien (Widersprüche) zu. Dies führte zur Kritik an der Cantorschen Mengenlehre und zur Entstehung anderer Konzepte (z.B. Typen- bzw. stufentheoretischer Aufbau der Mengenlehre, Klassentheorie, ...)

Beispiel: Russelsche Antinomie (B.Russel 1872 - 1970)

R = { M: M Menge  M  M } ist offenbar eine Cantormenge.
Dann gilt: R  R R  R          Widerspruch!

	zurück zu Potenzmengen	weiter zu Mengenalgebra