Mengen "gleicher Sorte", das heißt Teilmengen ein und derselben "Universalmenge" E, werden per Mengenoperationen miteinander verknüpft. Man beachte die Analogien zur Aussagenlogik.
Definition
1: Es
seien A, B ![]() P(E).
Dann heißt:
P(E).
Dann heißt:
| 1.
A |
Vereinigungsmenge von A und B |
| 2. A |
Durchschnittsmenge von A und B |
| 3. A \ B = {x:
x |
Differenzmenge A - B |
| 4. CE(A)
= {x: x |
Komplement von A (~A, falls E aus dem Zusammenhang bekannt) |
| 5. A |
symmetrische Differenz |
Bemerkungen:
| 1. A, B heißen disjunkt
(elementfremd), wenn A |
| 2. A \ B = A |
| 3. A |
Verallgemeinerungen:
Allgemeine Vereinigung und allgemeiner Durchschnitt:
Beispiel: A beliebig,- Menge von Mengen (Mengensystem)
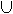
= {x:
x
M} ;
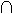
= {x:
x
M}
Zusammenfassung:
Betrachtet man eine Menge
M zusammen mit einer Menge ![]() von Operationen auf M, das heißt eine Gesamtheit [M,
von Operationen auf M, das heißt eine Gesamtheit [M,![]() ],
so spricht man von einer Algebra bzw. algebraischen Struktur.
],
so spricht man von einer Algebra bzw. algebraischen Struktur.
Hier: Mengenalgebren, wobei
A | B = ~(A ![]() B).
B).
Die in der Mengenalgebra geltenden Rechengesetze heißen Axiome der Algebra. Man erkennt starke Analogien bei den Axiomen zwischen Mengenalgebra und Aussagenlogik.= [P(E),
,
,
, \,
]
[P(E),
,
,
]
[P(E), | ]
Definition 2: (Zusammenhänge zwischen Mächtigkeiten und den Mengenoperationen)
Es seien A, B, C endliche
Mengen.
# M = n ![]()
![]() genau dann, wenn eine Bijektion von M auf { 0, 1, 2, ... , n-1} existiert.
genau dann, wenn eine Bijektion von M auf { 0, 1, 2, ... , n-1} existiert.
Dann gilt:
Satz 1:
Für alle Mengen A, B, C ![]() P(E) gelten die folgenden Rechenregeln der Mengenalgebra bzw. weiteren
Beziehungen:
P(E) gelten die folgenden Rechenregeln der Mengenalgebra bzw. weiteren
Beziehungen:
1. AFolgerung 1 (Gesetze für die Differenz)B = B
A
A
B = B
A
(Kommutativität vonund
)
2. A(B
C) = (A
B)
C
A
(B
C) = (A
B)
C
(Assoziativität vonund
)
3. AA = A
A
A = A
(Idempotenz vonund
)
4. A(A
B) = A
(A
B) = A
(Absorption/ Verschmelzung)
5. A(B
C) = (A
B)
(A
C)
A
(B
C) = (A
B)
(A
C)
(linksseitige Distributivität vongegenüber
und von
gegenüber
;
wegen 1. folgt hieraus sofort die beidseitige Distributivität)
6. A
= A
E = A
A

=
A
E = E
7. A
A = E
A

A =
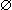

A = A
E =
= E
8.(A
B) =
A
B
(A
B) =
A
B
(de Morgan'sche Gesetze)
9. AA
B
A
B
A
10. AB
B
A
11. AB
A
B = B
A
B = A
12. AB
A
C
B
C
A
C
B
C
(Monotonie)
Für alle Mengen A, B, C ![]() P(E) gelten die folgenden Gesetze bezüglich der Mengendifferenz:
P(E) gelten die folgenden Gesetze bezüglich der Mengendifferenz:
1. (AFolgerung 2(Gesetze für die symmetrische Differenz)B) \ C = (A \ C)
(B \ C)
(rechtsseitige Distributivität von \ gegenüber)
2. (AB) \ C = (A \ C)
(B \ C)
(rechtsseitige Distributivität von \ gegenüber)
3. A \ (BC) = (A \ B)
(A \ C)
4. A \ (BC) = (A \ B)
(A \ C)
5. A \ (B \ C) = (A \ B)(A
C)
6. A \= A
A \ A =
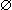
7. A \ (A \ B) = AB
Für alle Mengen A, B, C ![]() P(E) gelten die folgenden Gesetze bezüglich der symmetrischen Differenz:
P(E) gelten die folgenden Gesetze bezüglich der symmetrischen Differenz:
1. AA =
A
= A
2. AB = B
A
(Kommutativität von)
3. A(B
C) = (A
B)
C
(Assoziativität von)
4. (AB)
C = (A
C)
(B
C)
(Distributivität vonbezüglich
)
5. AB =
A
B = A
B
6.A
B = A
B
| zurück zu Mächtigkeiten | wieder zum Inhaltsverzeichnis |
| Mathematik für Medieninformatiker (c)2000 DeMorgan (Andreas Kumm, Julia Liebig, Klemens Neumann, Stephan Noske) |