Definition 1: (Inklusionsrelation)

Es seien A, B Mengen. Dann heißt A Teilmenge von B ( in Zeichen: A  B, B  A ) genau dann, wenn aus x  A stets x  B folgt.
        ( A  B  ( x  A  x  B ) )
Ferner heißt A echte Teilmenge von B ( A  B, B  A ) genau dann, wenn
        ( A  B ( x  B  x  A ) )
Folgerung:( M Menge   M )
Beweis: Es sei M beliebige Menge. Zu zeigen ist:   M  ( x    x  M )
             Da die Prämisse ( x   ) stets falsch ist, folgt die Wahrheit der Implikation.

Bemerkung: Veranschaulichung von Mengen durch Vennsche Diagramme (John Venn (1834-1923)) oder
                  Eulersche Kreise (Leonhard Euler (1707-1783)).

Eigenschaften der Inklusionsrelation:

1. A  A ; (Reflexivität von )
2. A  B  B  C  A  C ; (Transitivität von )
3. A  B  B  A  A = B ; (Antisymmetrie von )

Diese drei Eigenschaften erfüllt auch  in den Zahlenbereichen , , , . Im Unterschied zu  gilt für  im allgemeinen nicht die Eigenschaft der "Linearität":

( A  B  B  A  A = B ) (Vergleichbarkeit zweier Elemente).

Definition 2: (Mengengleichheit)       A = B  A  B  B  A

Beispiel:

1. A = { x: x    x² - 5x + 6 = 0 } ; B = { 2, 3 }

Dann gilt A = B, denn 1.) B  A, denn 2  A  3  A (Probe!)
                                2.) A  B, denn es gibt keine weiteren Lösungen.
(Satz von Vieta: x₁, x₂ sind Lösungen von x² + px + q = 0 genau dann, wenn x₁+ x₂= -p  x₁* x₂= q )
2. ist eindeutig bestimmt.

Beweis: (indirekt) Annahme:  und  sind leere Mengen.
                          Dann   , da  leere Menge.
                          Ebenso   , da  leere Menge. Daraus folgt  = .

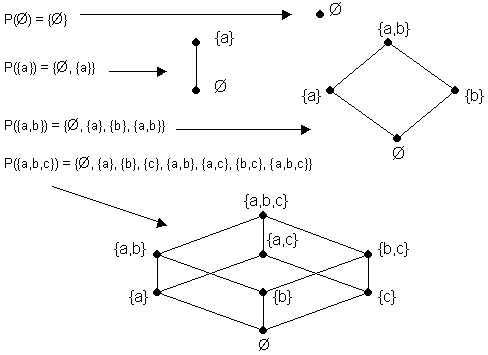
Es sei A Menge. Dann heißt P(A) = { x: x  A } Potenzmenge von A (Menge aller Teilmengen von A).

Beispiele:

• P() = { x: x   } = {} = { { } }
• P( {1} ) = { , {1} }
• P( {1, 2} ) = { , {1}, {2}, {1, 2} }
• P( {1, 2, 3} ) = { , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }

1. Die Potenzmenge einer beliebigen Menge ist nie leer. (, A  P(A) )
2. Kein einziges Element von A ist zugleich Element von P(A)! (P(A) ist Menge höheren Typs - Mengensystem)
3. Hat A genau n Elemente, so hat P(A) genau 2ⁿ- Elemente. (daher der Name Potenzmenge)

Veranschaulichung der Inklusionsrelation (für endliche Mengen) mittels Hasse-Diagrammen:

In einem Hasse-Diagramm zeichnet man

• Mengen mit gleicher Elementezahl auf gleiche Höhe
• zwischen Mengen N, M wird eine Kante angebracht, wenn N  M  N  N'  N'  M

	zurück zur Mengendefinition	weiter zu Mächtigkeiten

Mathematik für Medieninformatiker (c)2000 DeMorgan Group (Andreas Kumm, Julia Liebig, Klemens Neumann, Stephan Noske)